David McKillop: Mental Math Strategies in Middle Years
Today was day one of a two-day professional development session I’m attending as part of my Professional Growth Plan for the 2013-2014 school year. The sessions, presented by David McKillop, focus on mental math strategies (today) and assessment practices (tomorrow). David has over 30 years experience in the education field and is currently involved with Pearson’s “First Steps” and “Numeracy Nets” programs.
I haven’t developed a passion for math the same way I have for social studies and earth sciences but I felt that David’s presentation was very engaging (there was even singing!?) and I’m walking away with several strategies that I can utilize in my classroom immediately.
David introduced his session by discussing the concept of “math tourists“. These are our students who see the information, pass it by, maybe discuss it once or twice, but never truly take ownership of it. He mentioned that a lot of times our students focus more on the physical numbers that they recognize as opposed to the meaning behind the operation, which is why we have students misapplying strategies because they don’t understand the background behind why they are doing what they are doing.
The first half of the day was devoted to multiplication strategies while the second half provided strategies for division, estimation, & percentages. Here are some of the notes I took throughout the day:
1 ) knowledge of your multiplication facts
2 ) an understanding of properties
– associative property
– distributive property
3 ) an understanding of the meaning of multiplication
4 ) an understanding of place value
– when multiplying using standard algorithms we often
hear students immediately say something like, “I’m
carrying the 5″. No, you are actually carrying 50.
5 ) an ability to partition numbers
** teach knowledge of strategies that will go into long-term memory,
NOT quick tricks that are forgotten next week
Multiplication Strategies
1 ) Front-end Strategy
(ex) 6 x 59 = (6 x 50) + (6 x 9) = 300 + 54 = 354
2 ) Compensation Strategy
(ex) 6 x 60 = (6 x 60) – 6 = 360 – 6 = 354
3 ) Standard Algorithm
(ex) 59
x6
4 ) Using Compatible Factors
(ex) 50 x 46 x 2 = (50 x 2) x 46 = 100 x 46 = 4600
– Requires an understanding of the associative property
– Think, what will get me to a benchmark number like 100
5 ) Finding Compatible Factors
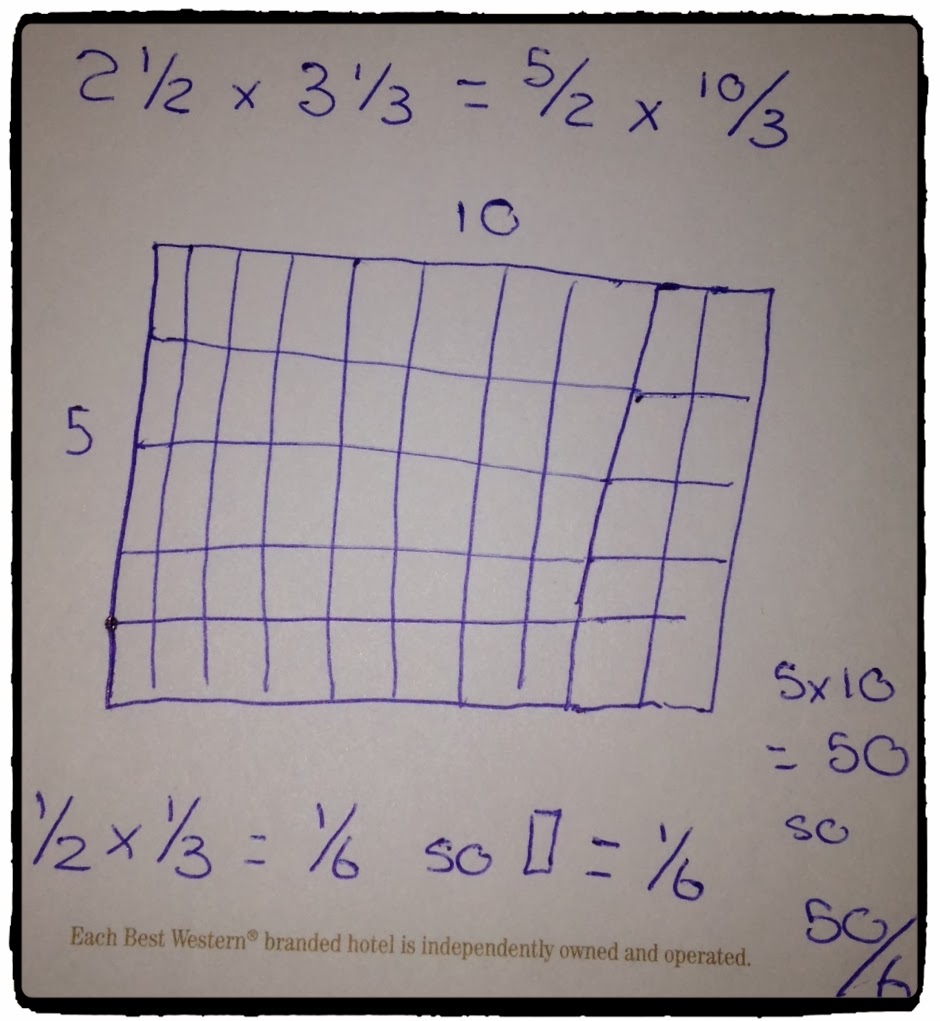
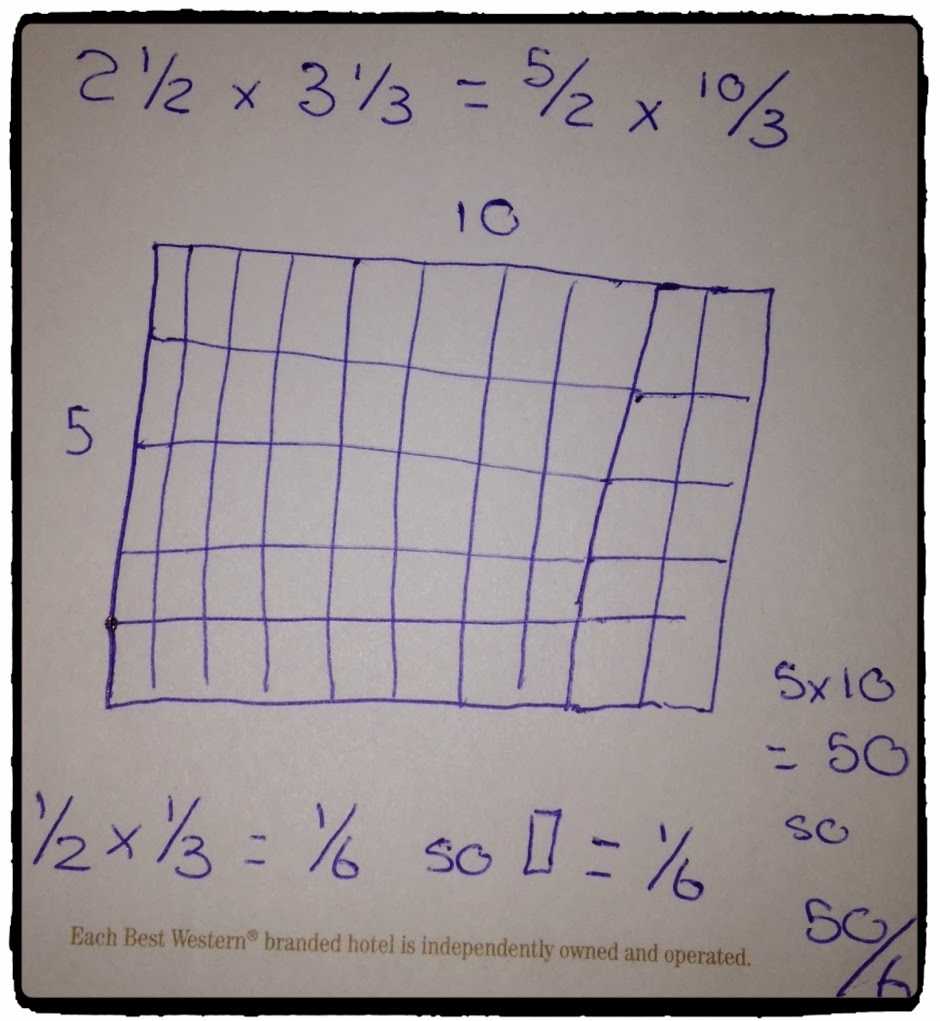
(ex) 25 x 48 = 25 x (4 x 12) = (25 x 4) x 12 = 100 x 12 = 1200
6 ) Halving & Doubling
(ex) 28 x 50 = (0.5 x 28) x (50 x 2) = 14 x 100 = 1400
* A good way to have students “discover” strategies is to present
them with a problem and have them share what steps they used
to find an answer. (students usually share all these strategies
except halving and doubling)
Multiplication Facts
– your multiplication facts provide the basis of all mental math
strategies & they facilitate the development of all other math
concepts as you use multiplication, in some depth, in all units
– your working memory can retrieve 7-10 items at one time &
we really expect students to be able to bring ALL their
multiplication facts at one time?
– we want our facts to be clustered in groups that can be
retrieved by strategies
– so students can remember 6-8 strategies rather than 100
discrete facts
Resources
Mental Math Support Booklets
Mental Math Support Videos